Why pooling layers in deep learning can cause problems

Pooling layers are omnipresent in today’s computer vision deep learning models. They reduce the size of the feature maps from layer to layer and thereby reduce the number of calculations needed. Still, there is an often overlooked problem with them. Let’s assume a binary classifier in the following discussion. Such a classifier shows a fluctuating output due to the pooling layers when the input image gets shifted. If the network has strong response (close to 100% class-score) to the input these fluctuations usually do not hurt. However, in the case of a weak response (slightly above 50%), these fluctuations can produce alternating class-outputs when the input gets shifted.
This article shows a classifier that exhibits such a behavior, analyzes the reasons for it, and finally lists possible solutions.
Pooling — quick recap
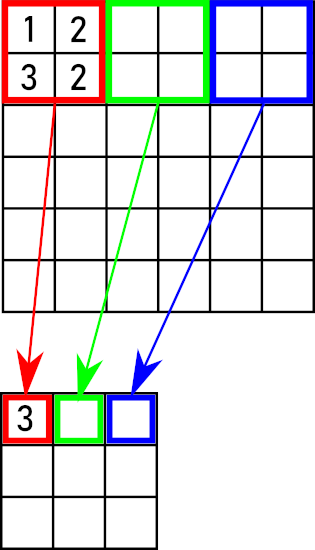
We will only consider the common max-pooling operation here. It is a sliding window operation: the window is located over a region (e.g., 2×2) of the input feature map and a single value (the maximum pixel value in the region) is output. This sliding window is moved across the whole input map, usually with a stride equal to the window size (e.g., stride of 2 in both x and y direction). Fig. 1 shows an illustration of the max-pooling operation.
A toy problem
Let’s build a binary classifier that distinguishes between circles and rectangles (see Fig. 2 for two dataset samples). We will then analyze the pooling layers with this model:
- The input is a 224×224 image
- There are three convolutional layers, where in the first two layers also the ReLU activation and max-pooling is applied (reducing the input image to 112×112 in the first hidden layer and 56×56 in the second one)
- Finally, the output feature map is averaged to get a single prediction value
- Cross entropy is used as a loss function, where the prediction is the averaged feature map value and the target is either 0 (rectangle) or 1 (circle)
- Code is available on GitHub

Analyzing the model
Now that we have a model trained to distinguish between rectangles and circles, let’s do a simple experiment. We will use a fixed-sized rectangle for this:
- Create a black image
- Render a rectangle of fixed size to some image location
- Compute prediction and save it for the current image location
- Repeat for all other image locations
So we’re essentially moving a rectangle around the image as shown in Fig. 3 and record how the network reacts to it.

This gives us a map showing the model output for each possible rectangle location in the image. As convolutional neural networks are advertised as shift-invariant models, we expect to see a constant prediction (close to 0 because rectangle is class 0). Fig. 4 shows the actual result.

As you can see, the model is able to correctly predict class 0 (all values <0.5), however, the output is not constant: it changes from pixel location to pixel location (between ~0 and ~0.1). It is clearly visible that there is a repeating pattern of the model output. By zooming in we see that it repeats every 4 pixels.
We wouldn’t even notice these things when only looking at the predicted class in this example. However, if the model is not that certain about the object in question (say, it outputs a value of 0.45), then these fluctuations of 0.1 would cause wrong class predictions for certain object locations. This especially gets evident when doing classification in video frames where objects move. Now that we can produce this possibly problematic behavior, let’s find the reason for it.
What causes this pattern
To keep things simple, let’s look at the 1D case of max-pooling as shown in Fig.5. Taking an input sequence (and assuming 0s on the left and right) and its shifted versions we wish to get the same (except shifted) output for both of them. However, this clearly is not the case:
- For the original input max-pooling outputs a sequence …, 1, 0, 2, 0, …
- For the sequence that was shifted by 1 we get …, 1, 1, 2, 2, …
- And finally, for the sequence shifted by 2 we again get …, 0, 1, 0, 2, … which is the original output shifted by 1

By doing a couple more shifts it is easy to see that all even shifts (0, 2, 4, …) produce the same (but shifted) output of the form …, 1, 0, 2, 0, …. The same is true for all odd shifts (1, 3, 5, …) which give …, 1, 1, 2, 2, …. So we get a repeating pattern here with a period of 2.
This example already shows that max-pooling is not shift-invariant in the 1D case, and generalizing to the 2D case is simple, just the drawings would get more complex. What does this mean for neural networks with pooling layers used for computer vision tasks? It means we can not expect the (intrinsically shift-variant) model to output the same prediction for an object moved across the image.
A closer look*
Can be skipped if you’re not interested in how this all connects to classic signal processing.
Max-pooling with window size W and stride W (e.g., W=2) can be split into two separate operations:
- Compute the maximum using a sliding window of size W that moves along the input sequence with a stride of 1
- Then, sample the intermediate sequence by taking every Wth element (e.g., for W=2 every second element is ignored)
In Fig. 5 an example is shown. It is easy to see that only using the sliding max-operation would not cause problems, as a shifted input sequence would simply lead to an equally shifted output sequence. However, as soon as sampling is involved this no longer is the case: take the white elements instead of the colored ones and you’ll get an entirely different sequence. In the field of signal processing it is a well-known property that sampling is not time-invariant (=shift-invariant). So the shift-variance of max-pooling layers arises from the shift-variance of sampling.
One last comment here: sometimes you read that aliasing causes the problems with pooling layers. Aliasing might also occur, however, it is not the reason for this effect. Even sampling from a perfectly anti-aliased signal like 1, 0, -1, 0, 1,… is not shift-invariant (either gives 1, -1, 1, …, or 0, 0, 0, …).

How to solve it?
Unfortunately, there is not a really satisfying solution to this problem I am aware of. Still, there are a couple of ways to improve robustness to shifts which are listed here:
- Get rid of all pooling layers (Azulay and Weiss): this might be a feasible solution for very small networks (e.g., for MNIST-style inputs).
- Add data augmentation that trains the model to be robust against small shifts (Azulay and Weiss): it is reported that the model only learns to be shift-invariant for inputs similar to the ones the model saw during the training phase.
- Apply a low-pass filter before sampling (Zhang): the classic approach to tackle aliasing. As mentioned, shift-variance is not caused by aliasing, still blurring the input makes the shifted outputs more similar to each other and thereby increases robustness.
- Try to always choose the “proper” sample grid (Chaman): there is more than one possible sample grid (e.g., we could sample at locations 0, 2, 4, … or alternatively at 1, 3, 5, …). If the input moves and we accordingly move the sample grid, we are able to always get the same (only shifted) output. This approach completely solves the problem in the ideal case. However, in a real scenario it can still fail (border effects, method of grid selection, …).
Overall, the best option is to be aware of this possibly problematic property. If you ever encounter it you can try the solutions listed above and see which one works best.
Conclusion
Pooling layers are used in almost every computer vision deep learning model today. They do a good job at reducing feature map sizes, however, at the same time they introduce shift-variance into the neural network.
I recommend the following publications if you want to take a deeper dive into the topic:
- Azulay and Weiss
- Zhang
- Chaman
- Lyons — Understanding Digital Signal Processing
